Sampling-Based Robust State Estimation for Deterministic Safety Controllers
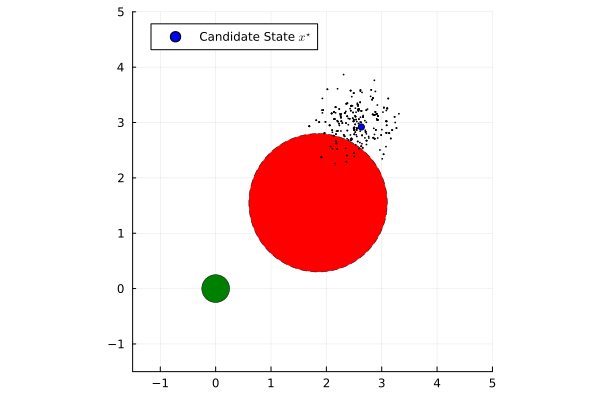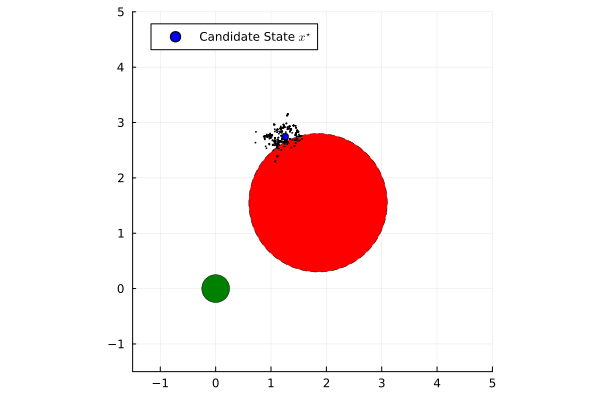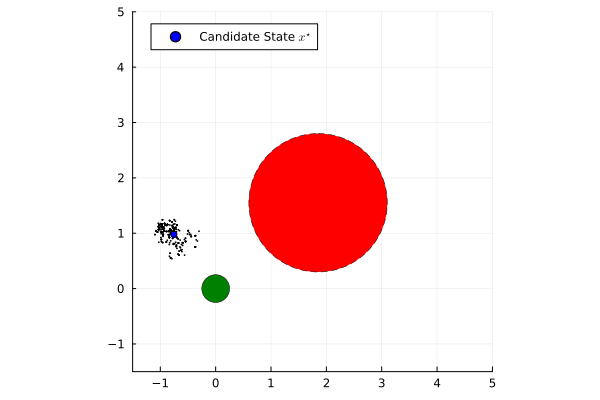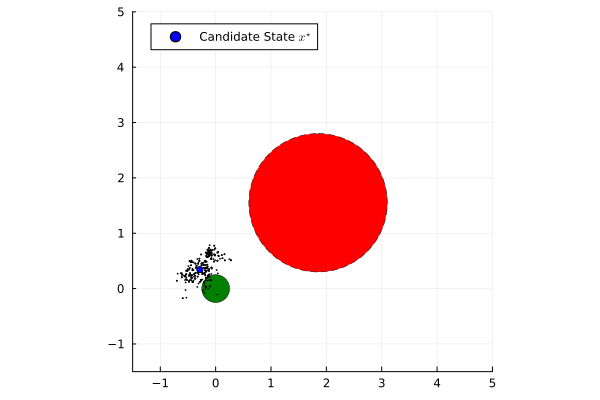
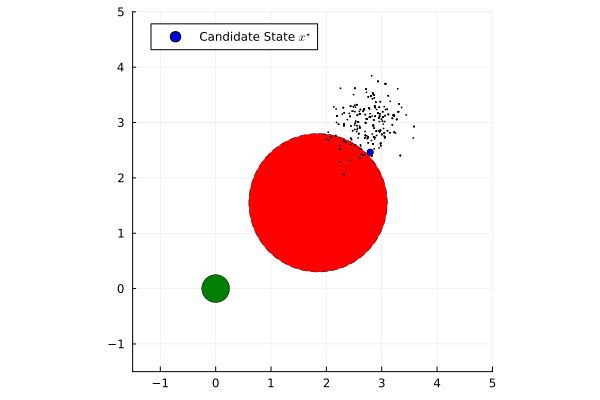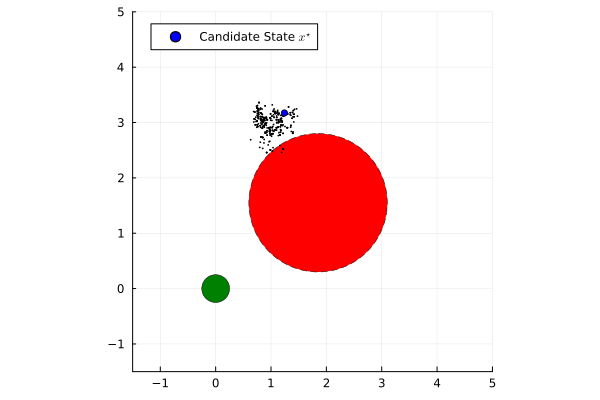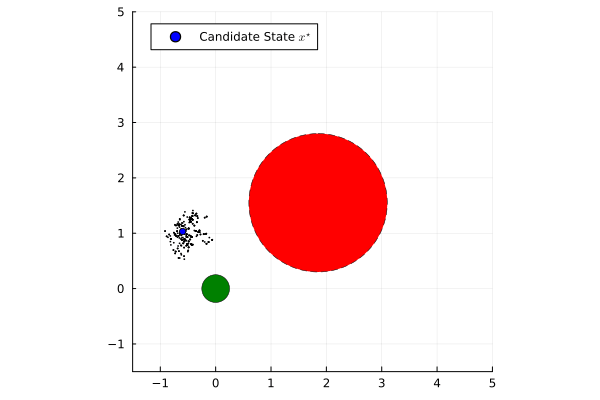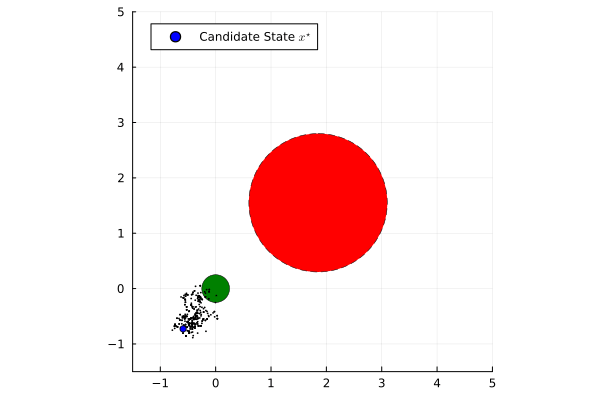
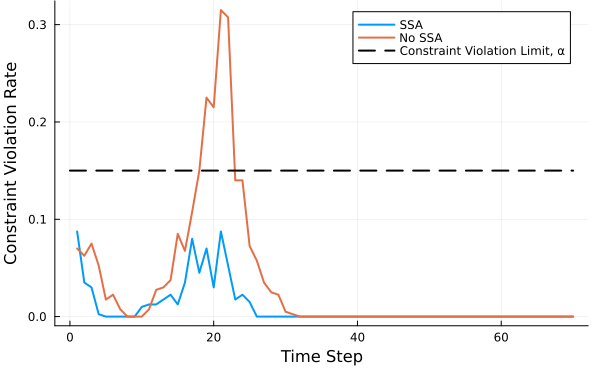
Established safety frameworks such as Hamilton-Jacobi Reachability and Control Barrier Functions provide powerful formal guarantees for performance and safety of dynamical systems. However, they traditionally assume perfect knowledge of the state and deterministic state transitions. In the case that there is process or measurement uncertainty within the system, these formal guarantees are compromised.
To address this limitation, this project leverages a Nested Monte Carlo method from stochastic Model Predictive Control. This approach selects the best-performing state estimate from candidates generated by a particle filter by optimizing a prescribed finite-horizon cost function while satisfying state and input constraints. The state estimate that minimizes the cost is then used in Certainty Equivalence feedback control. When combined with a Quadratic Program-based Control Barrier Function safety filter, this heuristic approach to stochastic optimal control provides a robust state estimate, improving the safety of deterministic controllers in stochastic settings while preserving performance objectives.